Code
library(ggplot2)
data("swiss")
ggplot(swiss) +
aes(x = Education, y = Fertility) +
geom_point(color = "purple") +
theme_minimal()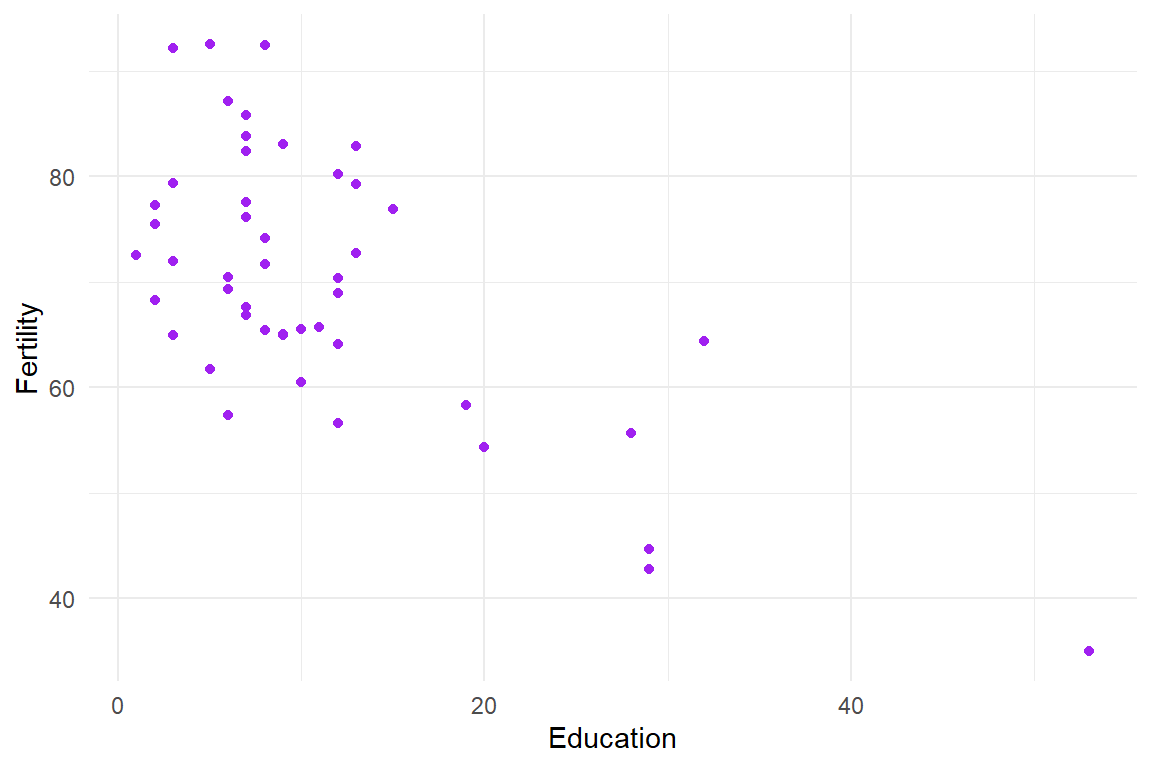
James E. Pustejovsky
January 15, 2025
I recently added some new utilities for calculating bootstrap confidence intervals to the simhelpers package. The functions are designed to make it a bit more convenient to implement Monte Carlo simulations of bootstrap CIs, including when using an extrapolation technique suggested by Boos & Zhang (2000), which I wrote about a while ago. With the latest update, the package now provides options for a bunch of different variants of bootstrap CIs, including:
These CI variants are also implemented in other packages. Most notably, all of them are implemented in boot (Canty & Ripley, 2024), the venerable R package companion to the Davison & Hinkley (1997) book on bootstrapping. Although very full-featured and widely used (it has 377 reverse dependencies!), the boot package does not offer a super-friendly user experience. Its output is a unwieldy, there are several quirks to its naming conventions, and its function for confidence interval calculations require the user to implement the bootstrap resampling calculations through boot::boot(), which is sometimes a bit awkward. Newer packages that provide some of the same methods include infer (Couch et al., 2021) and rsample (Frick et al., 2024). Both of these offer pipe-friendly workflows, but neither provides the full slate of CI variants. As with boot, these packages also lock in (or at least strongly nudge) the user to the package’s resampling tools. And none of the packages support a workflow for the Boos & Zhang (2000) extrapolation technique.
In this post, I’ll demonstrate the simhelpers implementation of these different CI variants with an example, compare the results to implementations in other packages, and then show how the simhelpers implementation can be used for the Boos & Zhang (2000) extrapolation technique.
Let me demonstrate the confidence intervals using a simple example of estimating a correlation. For illustrative purposes, I’ll use the swiss dataset of various socio-demographic measures of provinces in Switzerland from the late 19th century. I’ll look at the correlation between level of education and a measure of fertility:

Here is a function to calculate the sample correlation and its standard error (which is necessary for the studentized CIs):
r SE
-0.66378886 0.08247672 Using this function, we can generate a sample from the bootstrap distribution of the mean:
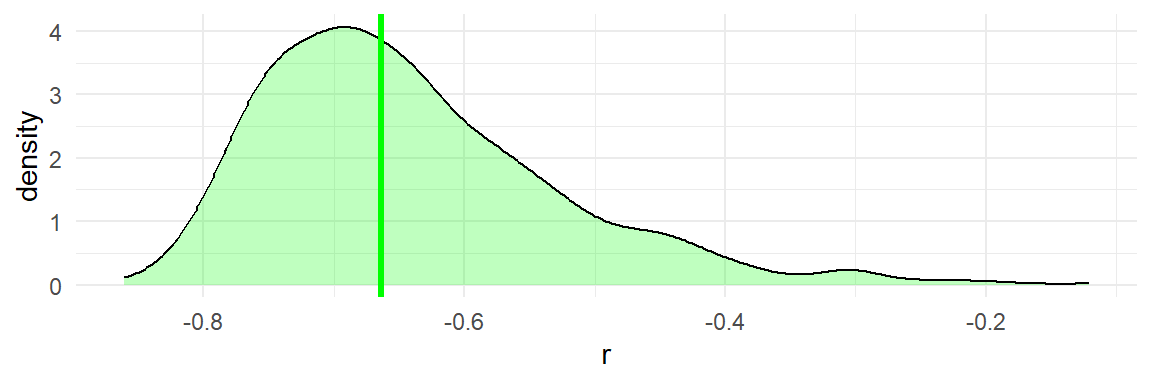
The bootstrap distribution of the sample correlations is clearly skewed and non-normal:
As a consequence of the asymmetry and non-normality of the bootstrap distribution, the different CI variants will produce discrepant intervals. The simhelpers function for calculating these intervals is as follows:
bootstraps type lower upper
1 999 normal -0.9061176 -0.4641111
2 999 basic -0.9571476 -0.5281576
3 999 student -0.8539880 -0.4535804
4 999 percentile -0.7994201 -0.3704302
5 999 bias-corrected -0.7994201 -0.3729852For the bias-corrected-and-accelerated interval, the function requires the user to provide a vector of the empirical influence values of each observation. I’ll calculate these using a jack-knife:
# leave-one-out jack-knife
jacks <- sapply(1:N, \(x) my_calc_cor(swiss[-x,])["r"])
# empirical influence
inf_vals <- mean(jacks) - jacks
# Now recalculate the bootstrap CIs
my_boot_CIs <- bootstrap_CIs(
boot_est = cors_boot$r,
boot_se = cors_boot$SE,
est = est["r"],
se = est["SE"],
influence = inf_vals,
CI_type = c("normal","basic","student","percentile","bias-corrected","BCa"),
format = "long",
seed = 20250111
)For sample correlation coefficients, another way to compute a confidence interval is via Fisher’s z-transformation, which is both normalizing and variance-stabilizing (so that the standard error of the point estimator does not depend on the parameter) under bivariate normality. The end-points of the CI on the Fisher z scale can then be back-transformed to the original scale. Here’s my “by-hand” calculation of this interval:
type lower upper
1 Fisher z -0.7987075 -0.4653206How do these various CIs compare? Here’s a graph illustrating all of the intervals:
CI_r$bootstraps <- 0
all_CIs <- rbind(my_boot_CIs, CI_r)
all_CIs$type <- factor(all_CIs$type, levels = c("Fisher z","BCa","bias-corrected","percentile","basic","student","normal"))
ggplot(all_CIs) +
aes(xmin = lower, xmax = upper, y = type, color = type) +
geom_vline(xintercept = est["r"], color = "green", linewidth = 1.2) +
geom_errorbar() +
theme_minimal() +
theme(legend.position = "none") +
labs(y = "")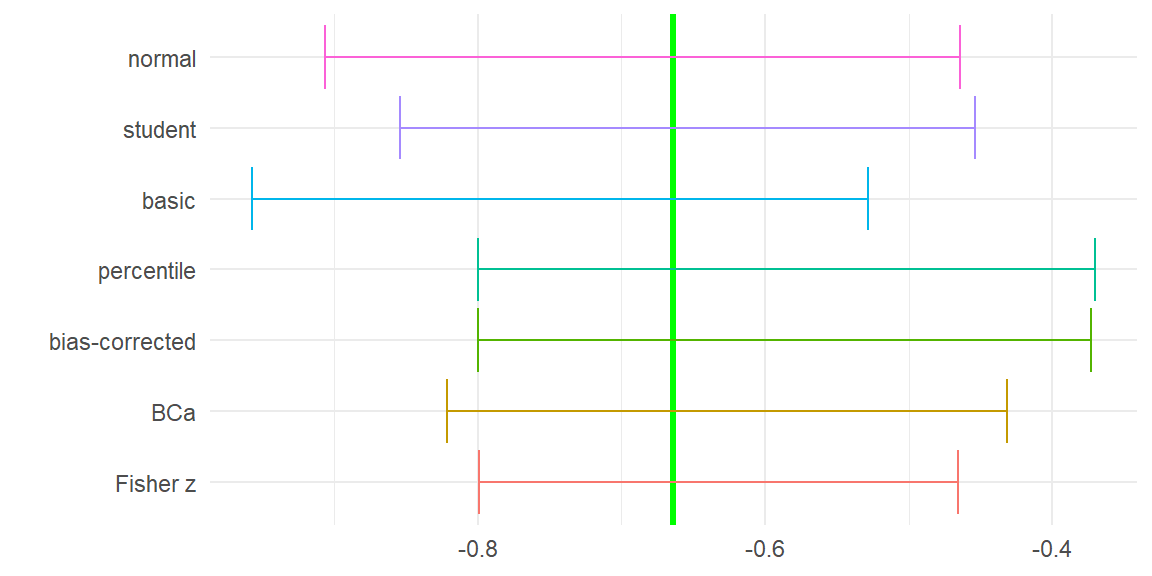
The various bootstrap intervals differ by quite a bit. The percentile and bias-corrected percentile intervals are wide and extend to smaller correlations than the other intervals. The basic interval is markedly different, extending to much higher correlations than any of the other intervals. The studentized and BCa intervals are closer to each other and come closer to matching the end-points of the Fisher z interval. It’s not necessarily the case that Fisher’s z interval is correct or optimal, unless the observations actually are drawn from a bivariate normal distribution. But it does seem suggestive that the studentized and BCa intervals are closer to agreeing with Fisher.
bootComparing the above calculations to what can be done with other packages is useful both as a validation exercise and as an illustration of the differences in workflow. Perhaps the most widely known R package for bootstrapping is Canty and Ripley’s boot package. Using it to obtain confidence intervals for a correlation requires running the bootstrap resampling process through its boot() function, which takes a bit of fiddling. First, I have to revise my calc_cor() function to take a subsetting index and to return the sampling variance instead of the standard error:
Now I can run it through boot() and compute some confidence intervals:
BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
Based on 999 bootstrap replicates
CALL :
boot.ci(boot.out = swiss_boots, type = "all")
Intervals :
Level Normal Basic Studentized
95% (-0.8854, -0.4754 ) (-0.9211, -0.5268 ) (-0.8362, -0.4502 )
Level Percentile BCa
95% (-0.8008, -0.4065 ) (-0.8111, -0.4518 )
Calculations and Intervals on Original ScaleThe package does not have an option for bias-corrected intervals (without acceleration) but it can be hacked by feeding a symmetrically distributed vector of influence points:
BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
Based on 999 bootstrap replicates
CALL :
boot.ci(boot.out = swiss_boots, type = "bca", L = -1:1)
Intervals :
Level BCa
95% (-0.8027, -0.4128 )
Calculations and Intervals on Original ScaleThese results will not align exactly with those reported above because they’re based on a different sample from the bootstrap distribution. To allow for direct comparison, I’ll recompute the intervals using the bootstrap sample stored in swiss_boots (and computing the influence values using the same method as used implicitly by boot.ci():
emp_inf_vals <- empinf(swiss_boots)
my_boot_CIs <- bootstrap_CIs(
boot_est = swiss_boots$t[,1],
boot_se = sqrt(swiss_boots$t[,2]),
est = swiss_boots$t0[1],
se = sqrt(swiss_boots$t0[2]),
influence = emp_inf_vals,
CI_type = c("normal","basic","student","percentile","bias-corrected","BCa"),
format = "long"
)It’d be nice to put the results from boot.ci() into a table to ease comparison with the output of bootstrap_CIs(), but its output is fairly untidy. Wrangling it takes a bit of work:
boot_boot_CI_tab <- data.frame(
type = c("normal","basic","student","percentile","bias-corrected","BCa"),
boot_lower = c(
boot_boot_CIs$normal[2],
boot_boot_CIs$basic[4],
boot_boot_CIs$student[4],
boot_boot_CIs$percent[4],
boot_BC_CI$bca[4],
boot_boot_CIs$bca[4]
),
boot_upper = c(
boot_boot_CIs$normal[3],
boot_boot_CIs$basic[5],
boot_boot_CIs$student[5],
boot_boot_CIs$percent[5],
boot_BC_CI$bca[5],
boot_boot_CIs$bca[5]
)
)
cbind(my_boot_CIs, boot_boot_CI_tab[,2:3]) bootstraps type lower upper boot_lower boot_upper
1 999 normal -0.8854201 -0.4754233 -0.8854201 -0.4754233
2 999 basic -0.9210706 -0.5268220 -0.9210706 -0.5268220
3 999 student -0.8361986 -0.4502460 -0.8361986 -0.4502460
4 999 percentile -0.8007557 -0.4065071 -0.8007557 -0.4065071
5 999 bias-corrected -0.8017628 -0.4135041 -0.8027344 -0.4127751
6 999 BCa -0.8110222 -0.4519353 -0.8111334 -0.4517669The first four intervals exactly match across packages. The bias-corrected and BCa intervals differ slightly because the packages use different interpolation methods for calculating percentiles that don’t correspond to integer positions in the sorted bootstrap sample.
inferThe infer package aims to provide a coherent grammar for statistical inference (including hypothesis testing and confidence intervals) based on resampling methods, following principles of tidy data and offering a pipe-friendly workflow. Again, I’ll need to repeat the bootstrap re-sampling in the package’s idiom:
library(dplyr)
library(infer)
set.seed(20250111)
# Compute point estimate
correlation_hat <- swiss |>
specify(Fertility ~ Education) |>
calculate(stat = "correlation")
# Compute bootstrap distribution
infer_boot <-
swiss |>
specify(Fertility ~ Education) |>
generate(reps = 999, type = "bootstrap") |>
calculate(stat = "correlation")I can then calculate studentized, percentile, and bias-corrected bootstrap CIs:
CI_normal <- get_confidence_interval(
infer_boot, type = "se",
point_estimate = correlation_hat, level = 0.95
)
CI_percentile <- get_confidence_interval(
infer_boot, type = "percentile",
level = 0.95
)
CI_biascorrected <- get_confidence_interval(
infer_boot, type = "bias-corrected",
point_estimate = correlation_hat, level = 0.95
)
infer_CIs <-
bind_rows(
normal = CI_normal,
percentile = CI_percentile,
`bias-corrected` = CI_biascorrected,
.id = "type"
)For comparison purposes, I’ll once again need to re-compute the intervals with bootstrap_CIs(), this time with the infer bootstrap sample:
bootstraps type lower upper lower_ci upper_ci
1 999 normal -0.9052953 -0.4614019 -0.8857356 -0.4418421
2 999 percentile -0.8030248 -0.3487307 -0.8027752 -0.3507277
3 999 bias-corrected -0.8027620 -0.3487307 -0.8027066 -0.3504208The results do not exactly match across packages. For the normal interval, the difference occurs because the simhelpers implementation (like the boot implementation) includes a bias-correction term that shifts the interval by the difference between the point estimate and the average bootstrap estimate, which infer does not do. The very small differences in the percentile and bias-corrected intervals are due to the use of different interpolation methods for calculating percentiles.
rsampleOkay, one last time, this time using the rsample package by Frick et al. (2024). I’ll first need to re-work my correlation calculation to provide a data.frame with columns called term, estimate, and std.error, and also ensure that the function allows for extra arguments with ....
Now I can generate a bootstrap distribution using bootstraps, setting apparent = TRUE to include calculation of the point estimate and analytical standard error. I’ll use about 2000 bootstraps here to avoid an automated warning message.
The resample package provides functions for calculating percentile, studentized, and BCa intervals. I’ll do all three:
Now I’ll redo the interval calculations with bootstrap_CIs():
# just the point estimate
rsample_apparent <-
rsample_boots %>%
filter(id == "Apparent") %>%
unnest(r)
# just the bootstraps
rsample_boots <-
rsample_boots %>%
filter(id != "Apparent") %>%
unnest(r)
# jack-knife to get empirical influence values
inf_vals <-
swiss %>%
loo_cv() %>%
mutate(r = map(splits, rsample_calc_cor)) %>%
unnest(r) %>%
mutate(
inf_val = rsample_apparent$estimate - estimate
) %>%
pull(inf_val)
# calculate bootstrap CIs
my_rsample_CIs <-
bootstrap_CIs(
boot_est = rsample_boots$estimate,
boot_se = rsample_boots$std.error,
est = rsample_apparent$estimate,
se = rsample_apparent$std.error,
influence = inf_vals,
CI_type = c("student","percentile","BCa"),
format = "long"
)
# Compare
inner_join(my_rsample_CIs, rsample_CIs) bootstraps type lower upper .lower .upper
1 1999 student -0.8529496 -0.4470351 -0.8526882 -0.4484207
2 1999 percentile -0.8020261 -0.3725691 -0.8014797 -0.3731069
3 1999 BCa -0.8194484 -0.4326284 -0.8191845 -0.4324908All checks out, with small differences due to the method used to interpolate percentiles and how the acceleration constant is calculated.
Although rsample does not provide the full set of bootstrap CI variants, the three it does include are probably the most useful ones. The option to include the original sample estimate as an additional result in the bootstraps object is also quite nice, and the functions smoothly handle computing bootstraps for each of several terms (such as multiple regression coefficient estimates from a given model). However, the workflow enforced by rsample does seem to have a big downside with respect to memory management. Taking a bootstrap sample with loo_cv() creates a near-copy of the dataset for every row of the original dataset. These could get to be quite large objects:
6464 bytes403696 bytes8561488 bytesEspecially for large datasets, it would be much more memory-efficient to roll together the re-sampling step and the estimation step or to store only the resampled row indices rather than copies of the full dataset.
One big reason that I implemented all these boostrap CI variants in simhelpers is to assist with running Monte Carlo simulations of bootstrap procedures. The main novel feature of my implementation is that bootstrap_CIs() can compute not just one interval, but a collection of several intervals using different-sized subsamples of bootstrap replicates. The number of bootstrap replicates to use in each interval can be specified by providing a vector to the B_vals argument, as follows:
bootstraps type lower upper
1 99 BCa -0.8187481 -0.4565992
2 199 BCa -0.8536818 -0.4314318
3 299 BCa -0.8163946 -0.4133028
4 399 BCa -0.8185373 -0.4314318
5 499 BCa -0.8264171 -0.4314478
6 599 BCa -0.8209467 -0.4317901
7 699 BCa -0.8231215 -0.4429049
8 799 BCa -0.8231215 -0.4314318
9 899 BCa -0.8213542 -0.4314318
10 999 BCa -0.8213542 -0.4314478In the context of a simulation study, this feature makes it feasible to compute coverage levels of a bootstrap CI for several different values of
Here is a small simulation to demonstrate how all this can work. I’ll generate samples of size
And the estimation function:
cor_CI <- function(
dat,
CI_type = "percentile",
B_vals = c(49, 99, 199, 299, 399)
) {
# point estimate
r_est <- cor(dat[,1], dat[,2])
N <- nrow(dat)
SE_r <- sqrt((1 - r_est^2)^2 / (N - 1))
# Fisher z CI
z <- atanh(r_est)
SE_z <- 1 / sqrt(N - 3)
CI_z <- z + c(-1, 1) * qnorm(0.975) * SE_z
# empirical influence if needed
if ("BCa" %in% CI_type) {
jacks <- sapply(1:N, \(x) cor(dat[-x,1], dat[-x,2]))
inf_vals <- r_est - jacks
} else {
inf_vals <- NULL
}
# bootstrap samples
r_boot <- replicate(max(B_vals), {
i <- sample(1:N, replace = TRUE, size = N)
r <- cor(dat[i,1], dat[i,2])
c(r, sqrt((1 - r^2)^2 / (N - 1)))
})
bs_CIs <- simhelpers::bootstrap_CIs(
boot_est = r_boot[1,],
boot_se = r_boot[2,],
est = r_est,
se = SE_r,
influence = inf_vals,
CI_type = CI_type,
B_vals = B_vals,
format = "wide-list"
)
tibble::tibble(
r = r_est,
SE = SE_r,
lo = tanh(CI_z[1]),
hi = tanh(CI_z[2]),
w = mean(r_boot < r_est),
a = sum(inf_vals^3) / (6 * sum(inf_vals^2)^1.5),
bs_CIs = bs_CIs
)
}
res <- cor_CI(dat, CI_type = c("percentile","student"))
res# A tibble: 1 × 7
r SE lo hi w a bs_CIs
<dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <btstr_CI>
1 0.788 0.0774 0.570 0.902 0.723 NaN <df [5 × 5]>Setting the argument format = "wide-list" in the call to generate_CIs() makes it convenient to store all the CIs in a nested list-column. Here’s the contents of bs_CIs:
bootstraps student_lower student_upper percentile_lower percentile_upper
1 49 0.6017501 0.9143423 0.5580763 0.8898411
2 99 0.5510270 0.8967928 0.6059297 0.9029773
3 199 0.5312326 0.9102482 0.5697594 0.9073084
4 299 0.5327977 0.8988743 0.6005613 0.9069798
5 399 0.5510270 0.9054740 0.5829886 0.9029773Now let me pass these functions to simhelpers::bundle_sim() so that I can replicate the data-generation and estimation calls as many times as I like. Calling the resulting function gives me 2000 replications of the whole process, where each replication involves generating
# bundle the data-generating and estimation functions
# into a simulation driver
sim_cor <- bundle_sim(r_t_bi, cor_CI)
# Run many replications
sim_reps <- sim_cor(
reps = 2000,
n = 25, rho = rho,
B_vals = c(49, 99, 199, 299, 399),
CI_type = c("normal","student","basic","percentile","bias-corrected", "BCa")
)
head(sim_reps)# A tibble: 6 × 7
r SE lo hi w a bs_CIs
<dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <btstr_CI>
1 0.507 0.152 0.140 0.752 0.721 -0.0768 <df [5 × 13]>
2 0.866 0.0509 0.717 0.940 0.747 0.0203 <df [5 × 13]>
3 0.679 0.110 0.388 0.847 0.767 0.112 <df [5 × 13]>
4 0.677 0.111 0.385 0.846 0.766 0.0941 <df [5 × 13]>
5 0.807 0.0711 0.605 0.912 0.754 0.0252 <df [5 × 13]>
6 0.813 0.0691 0.616 0.914 0.746 -0.00761 <df [5 × 13]>Now I’ll summarize across replications to evaluate the coverage rates of each set of confidence intervals. For the Fisher intervals, simhelpers::calc_coverage() does the trick, but for the bootstrap intervals I need to use simhelpers::extrapolate_coverage() because each replication is a specially structured set of multiple confidence intervals with different values of
perf <-
sim_reps %>%
summarize(
calc_absolute(estimates = r, true_param = rho, criteria = "bias"),
calc_coverage(lower_bound = lo, upper_bound = hi, true_param = rho),
extrapolate_coverage(
CI_subsamples = bs_CIs, true_param = rho,
B_target = 1999,
nested = TRUE, format = "long"
)
)
# Bias and Fisher interval
perf %>%
select(bias, coverage, width)# A tibble: 1 × 3
bias coverage width
<dbl> <dbl> <dbl>
1 -0.00879 0.919 0.377The correlation has a slight negative bias. The Fisher
# A tibble: 6 × 4
CI_type bootstraps boot_coverage boot_width
<chr> <dbl> <dbl> <dbl>
1 percentile 49 0.896 0.371
2 percentile 99 0.914 0.390
3 percentile 199 0.921 0.400
4 percentile 299 0.917 0.391
5 percentile 399 0.924 0.396
6 percentile 1999 0.926 0.400In addition to the coverage rates and average widths of intervals based on between 49 and 399 bootstraps, the results also include performance summaries for intervals with
boot_performance_top <- filter(boot_performance, bootstraps == 1999)
ggplot(boot_performance) +
aes(x = bootstraps, y = boot_coverage, color = CI_type) +
scale_x_continuous(breaks = c(49,99,199,399,1999), transform = "reciprocal") +
scale_y_continuous(limits = c(0.8,1.0), expand = expansion(0, 0), sec.axis = dup_axis(name = "")) +
geom_hline(yintercept = 0.95, linetype = "dashed") +
geom_hline(data = perf, aes(yintercept = coverage), color = "darkgrey") +
geom_point() +
ggrepel::geom_label_repel(
data = boot_performance_top,
aes(label = CI_type),
nudge_x = -0.004
) +
geom_smooth(method = "lm", formula = y ~ x, se = FALSE) +
theme_minimal() +
theme(legend.position = "none") +
labs(
x = "Bootstraps (B)",
y = "CI coverage rate"
)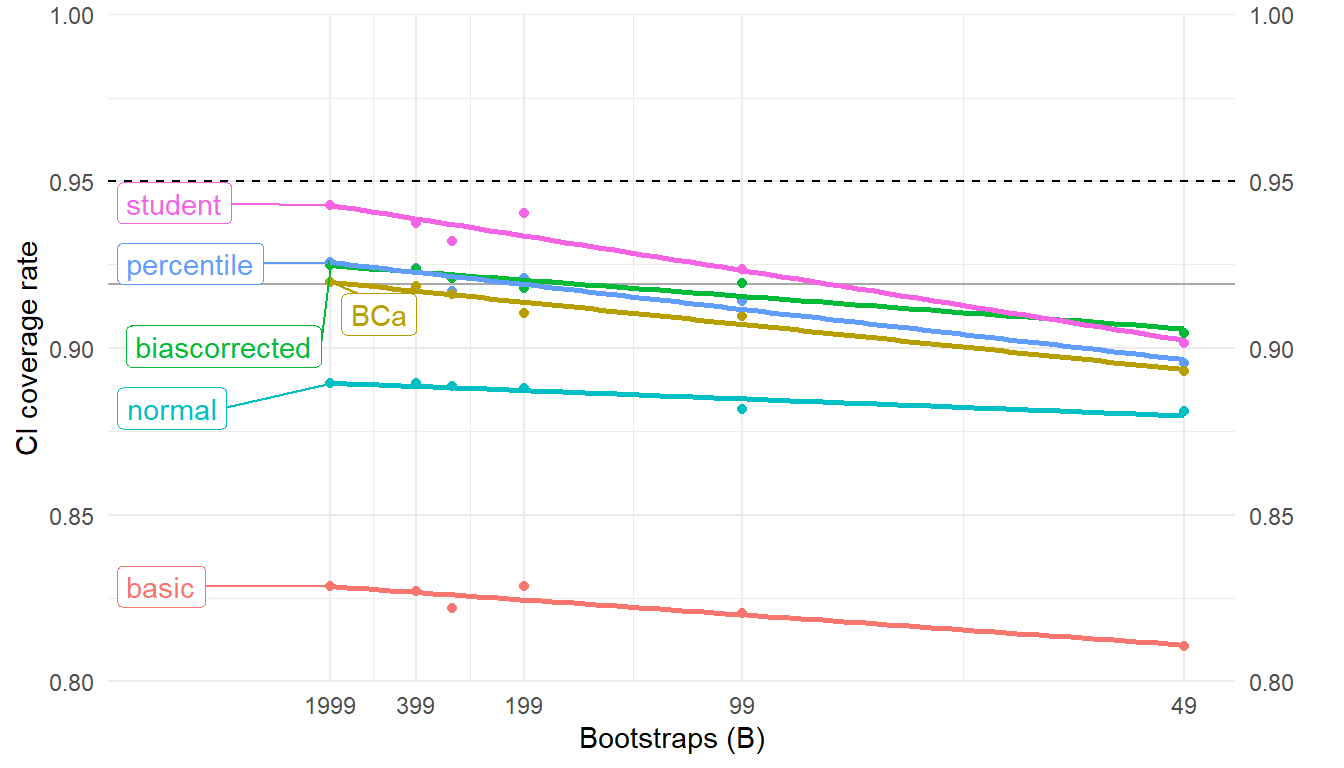
The studentized interval gets very close to the nominal coverage level with
Perhaps this is because, for this simple problem, the extra machinery of the bias and acceleration corrections might not be needed or the corrections cannot be estimated accurately enough with a sample of this size.
Here’s the average widths of each variant:
boot_performance_bottom <- filter(boot_performance, bootstraps == 49)
ggplot(boot_performance) +
aes(x = bootstraps, y = boot_width, color = CI_type) +
scale_x_continuous(breaks = c(49,99,199,399,1999), transform = "reciprocal") +
geom_hline(data = perf, aes(yintercept = width), color = "darkgrey") +
geom_point() +
ggrepel::geom_label_repel(
data = boot_performance_bottom,
aes(label = CI_type),
nudge_x = 0.004
) +
geom_smooth(method = "lm", formula = y ~ x, se = FALSE) +
theme_minimal() +
theme(legend.position = "none") +
labs(
x = "Bootstraps (B)",
y = "Average CI width"
)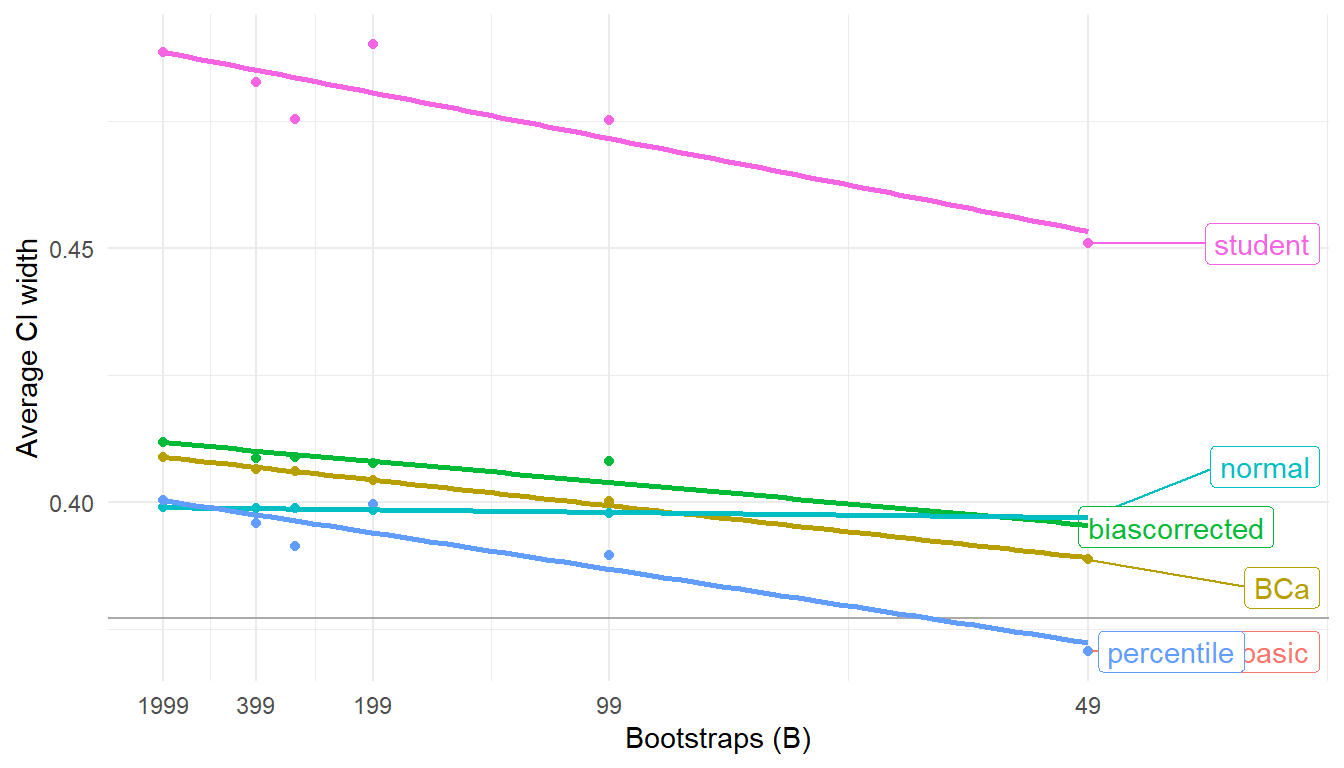
The near-nominal coverage rate for the studentized interval comes with an increased width. The percentile and basic CIs have identical widths because they’re based on the same percentiles, just used in different ways. Notably, the percentile interval has shorter average width than the bias-corrected or BCa intervals, even though it also has better coverage.
This particular problem is perhaps not the most compelling way illustrate Boos and Zhang’s extrapolation method because it would fairly simple to just compute a larger number of bootstraps and not worry about the complications of computing a bunch of extra CIs and extrapolating. Here’s some timing comparisons. First, the brute-force approach of just computing
library(tictoc)
tic()
perf_1999 <-
sim_cor(
reps = 500,
n = 25, rho = 0.75,
B_vals = 1999,
CI_type = c("normal","student","basic","percentile","bias-corrected", "BCa")
) %>%
unnest(bs_CIs) %>%
pivot_longer(
c(ends_with("_lower"), ends_with("_upper")),
names_pattern = "(.+)_(.+)",
names_to = c("CI_type",".value")
) %>%
group_by(CI_type) %>%
summarize(
calc_coverage(lower_bound = lower, upper_bound = upper, true_param = 0.75)
)
toc()30.95 sec elapsedCompare that to doing 500 replications, each with 399 bootstraps but computing 5 confidence intervals each time and then extrapolating out to
tic()
perf_extra <-
sim_cor(
reps = 500,
n = 25, rho = 0.75,
B_vals = c(49, 99, 199, 299, 399),
CI_type = c("normal","student","basic","percentile","bias-corrected", "BCa")
) %>%
summarize(
extrapolate_coverage(
CI_subsamples = bs_CIs, true_param = rho,
B_target = 1999,
nested = TRUE, format = "long"
)
)
toc()11.28 sec elapsedThere is some time savings, but perhaps not worth the extra hassle in this instance. The extrapolation method is much more useful when the statistic calculated on each bootstrap re-sample takes a relatively long time to compute, so that using only a fraction of the bootstraps (399 versus 1999, in this example) substantially reduces the total compute time.
---
title: Bootstrap confidence interval variations
date: '2025-01-15'
categories:
- programming
- Rstats
- bootstrap
code-fold: show
code-tools: true
toc: true
bibliography: "references.bib"
csl: "../apa.csl"
---
I recently added some new utilities for calculating bootstrap confidence intervals to the [`simhelpers` package](https://meghapsimatrix.github.io/simhelpers/).
The functions are designed to make it a bit more convenient to implement Monte Carlo simulations of bootstrap CIs, including when using an extrapolation technique suggested by @boos2000MonteCarloEvaluation, which [I wrote about a while ago](/posts/Simulating-bootstrap-CIs/).
With the latest update, the package now provides options for a bunch of different variants of bootstrap CIs, including:
* the normal CI, which uses bootstrapping to estimate a standard error and bias-correction, then takes plus or minus a normal critical value times the SE;
* the studentized CI, which uses the bootstrap distribution of a t-statistic rather than the point estimator;
* the percentile CI, which takes percentiles of the bootstrap distribution as the end-points of the CI;
* the so-called "basic" CI, which is similar to the percentile CI but pivots the bootstrap distribution around the point estimator;
* a bias-corrected version of the percentile CI;
* Efron's [-@efron1987better] bias-corrected-and-accelerated CI, which is supposed to provide more accurate coverage levels than alternative CIs for some classes of estimators.
These CI variants are also implemented in other packages.
Most notably, all of them are implemented in [`boot`](https://cran.r-project.org/package=boot) [@bootpkg], the venerable R package companion to the @Davison1997bootstrap book on bootstrapping.
Although very full-featured and widely used (it has `r crandep::get_dep("boot", "all", reverse = TRUE) |> nrow()` reverse dependencies!), the `boot` package does not offer a super-friendly user experience.
Its output is a unwieldy, there are several quirks to its naming conventions, and its function for confidence interval calculations require the user to implement the bootstrap resampling calculations through `boot::boot()`, which is sometimes a bit awkward.
Newer packages that provide some of the same methods include [`infer`](https://infer.netlify.app/) [@Couch2021infer] and [`rsample`](https://rsample.tidymodels.org/) [@rsamplepkg].
Both of these offer pipe-friendly workflows, but neither provides the full slate of CI variants.
As with `boot`, these packages also lock in (or at least strongly nudge) the user to the package's resampling tools.
And none of the packages support a workflow for the @boos2000MonteCarloEvaluation extrapolation technique.
In this post, I'll demonstrate the `simhelpers` implementation of these different CI variants with an example, compare the results to implementations in other packages, and then show how the `simhelpers` implementation can be used for the @boos2000MonteCarloEvaluation extrapolation technique.
# Bootstrap confidence intervals for a mean
Let me demonstrate the confidence intervals using a simple example of estimating a correlation. For illustrative purposes, I'll use the `swiss` dataset of various socio-demographic measures of provinces in Switzerland from the late 19th century. I'll look at the correlation between level of education and a measure of fertility:
```{r}
#| code-fold: true
#| fig-width: 6
#| fig-height: 4
#| out-width: 75%
library(ggplot2)
data("swiss")
ggplot(swiss) +
aes(x = Education, y = Fertility) +
geom_point(color = "purple") +
theme_minimal()
```
Here is a function to calculate the sample correlation and its standard error (which is necessary for the studentized CIs):
```{r}
my_calc_cor <- function(x) {
r <- cor(x$Education, x$Fertility)
n <- nrow(x)
c(r = r, SE = sqrt((1 - r^2)^2 / (n - 1)))
}
est <- my_calc_cor(swiss)
est
```
Using this function, we can generate a sample from the bootstrap distribution of the mean:
```{r}
N <- nrow(swiss)
cors_boot <- replicate(999, {
i <- sample(1:N, replace = TRUE, size = N)
my_calc_cor(swiss[i,])
}) |>
t() |>
as.data.frame()
```
The bootstrap distribution of the sample correlations is clearly skewed and non-normal:
```{r}
#| code-fold: true
#| fig-width: 6
#| fig-height: 2
#| out-width: 75%
ggplot(cors_boot) +
aes(r) +
geom_density(fill = "green", alpha = 0.25) +
geom_vline(xintercept = est["r"], color = "green", linewidth = 1.2) +
theme_minimal()
```
As a consequence of the asymmetry and non-normality of the bootstrap distribution, the different CI variants will produce discrepant intervals.
The simhelpers function for calculating these intervals is as follows:
```{r}
library(simhelpers)
bootstrap_CIs(
boot_est = cors_boot$r,
boot_se = cors_boot$SE,
est = est["r"],
se = est["SE"],
CI_type = c("normal","basic","student","percentile","bias-corrected"),
format = "long"
)
```
For the bias-corrected-and-accelerated interval, the function requires the user to provide a vector of the empirical influence values of each observation. I'll calculate these using a jack-knife:
```{r}
# leave-one-out jack-knife
jacks <- sapply(1:N, \(x) my_calc_cor(swiss[-x,])["r"])
# empirical influence
inf_vals <- mean(jacks) - jacks
# Now recalculate the bootstrap CIs
my_boot_CIs <- bootstrap_CIs(
boot_est = cors_boot$r,
boot_se = cors_boot$SE,
est = est["r"],
se = est["SE"],
influence = inf_vals,
CI_type = c("normal","basic","student","percentile","bias-corrected","BCa"),
format = "long",
seed = 20250111
)
```
For sample correlation coefficients, another way to compute a confidence interval is via Fisher's z-transformation, which is both normalizing and variance-stabilizing (so that the standard error of the point estimator does not depend on the parameter) under bivariate normality. The end-points of the CI on the Fisher z scale can then be back-transformed to the original scale. Here's my "by-hand" calculation of this interval:
```{r}
z <- atanh(est["r"])
SE_z <- 1 / sqrt(N - 3)
CI_z <- z + c(-1, 1) * qnorm(0.975) * SE_z
CI_r <- data.frame(
type = "Fisher z",
lower = tanh(CI_z[1]),
upper = tanh(CI_z[2])
)
CI_r
```
How do these various CIs compare? Here's a graph illustrating all of the intervals:
```{r}
#| code-fold: true
#| fig-width: 6
#| fig-height: 3
#| out-width: 75%
CI_r$bootstraps <- 0
all_CIs <- rbind(my_boot_CIs, CI_r)
all_CIs$type <- factor(all_CIs$type, levels = c("Fisher z","BCa","bias-corrected","percentile","basic","student","normal"))
ggplot(all_CIs) +
aes(xmin = lower, xmax = upper, y = type, color = type) +
geom_vline(xintercept = est["r"], color = "green", linewidth = 1.2) +
geom_errorbar() +
theme_minimal() +
theme(legend.position = "none") +
labs(y = "")
```
The various bootstrap intervals differ by quite a bit.
The percentile and bias-corrected percentile intervals are wide and extend to smaller correlations than the other intervals.
The basic interval is markedly different, extending to much higher correlations than any of the other intervals.
The studentized and BCa intervals are closer to each other and come closer to matching the end-points of the Fisher z interval.
It's not necessarily the case that Fisher's z interval is correct or optimal, unless the observations actually are drawn from a bivariate normal distribution.
But it does seem suggestive that the studentized and BCa intervals are closer to agreeing with Fisher.
# Comparison to other packages
## `boot`
Comparing the above calculations to what can be done with other packages is useful both as a validation exercise and as an illustration of the differences in workflow.
Perhaps the most widely known R package for bootstrapping is Canty and Ripley's [`boot`](https://cran.r-project.org/package=boot) package.
Using it to obtain confidence intervals for a correlation requires running the bootstrap resampling process through its `boot()` function, which takes a bit of fiddling.
First, I have to revise my `calc_cor()` function to take a subsetting index and to return the sampling variance instead of the standard error:
```{r}
library(boot)
boot_calc_cor <- function(x, i = 1:nrow(x)) {
r <- cor(x$Education[i], x$Fertility[i])
n <- nrow(x[i,])
c(r = r, V = (1 - r^2)^2 / (n - 1))
}
```
Now I can run it through `boot()` and compute some confidence intervals:
```{r}
set.seed(20250111)
swiss_boots <- boot(swiss, boot_calc_cor, R = 999)
boot_boot_CIs <- boot.ci(swiss_boots, type = "all")
boot_boot_CIs
```
The package does not have an option for bias-corrected intervals (without acceleration) but it can be hacked by feeding a symmetrically distributed vector of influence points:
```{r}
boot_BC_CI <- boot.ci(swiss_boots, type = "bca", L = -1:1)
boot_BC_CI
```
These results will not align exactly with those reported above because they're based on a different sample from the bootstrap distribution.
To allow for direct comparison, I'll recompute the intervals using the bootstrap sample stored in `swiss_boots` (and computing the influence values using the same method as used implicitly by `boot.ci()`:
```{r}
emp_inf_vals <- empinf(swiss_boots)
my_boot_CIs <- bootstrap_CIs(
boot_est = swiss_boots$t[,1],
boot_se = sqrt(swiss_boots$t[,2]),
est = swiss_boots$t0[1],
se = sqrt(swiss_boots$t0[2]),
influence = emp_inf_vals,
CI_type = c("normal","basic","student","percentile","bias-corrected","BCa"),
format = "long"
)
```
It'd be nice to put the results from `boot.ci()` into a table to ease comparison with the output of `bootstrap_CIs()`, but its output is fairly untidy. Wrangling it takes a bit of work:
```{r}
boot_boot_CI_tab <- data.frame(
type = c("normal","basic","student","percentile","bias-corrected","BCa"),
boot_lower = c(
boot_boot_CIs$normal[2],
boot_boot_CIs$basic[4],
boot_boot_CIs$student[4],
boot_boot_CIs$percent[4],
boot_BC_CI$bca[4],
boot_boot_CIs$bca[4]
),
boot_upper = c(
boot_boot_CIs$normal[3],
boot_boot_CIs$basic[5],
boot_boot_CIs$student[5],
boot_boot_CIs$percent[5],
boot_BC_CI$bca[5],
boot_boot_CIs$bca[5]
)
)
cbind(my_boot_CIs, boot_boot_CI_tab[,2:3])
```
The first four intervals exactly match across packages.
The bias-corrected and BCa intervals differ slightly because the packages use different interpolation methods for calculating percentiles that don't correspond to integer positions in the sorted bootstrap sample.
## `infer`
The [`infer`](https://infer.netlify.app/) package aims to provide a coherent grammar for statistical inference (including hypothesis testing and confidence intervals) based on resampling methods, following principles of tidy data and offering a pipe-friendly workflow. Again, I'll need to repeat the bootstrap re-sampling in the package's idiom:
```{r}
library(dplyr)
library(infer)
set.seed(20250111)
# Compute point estimate
correlation_hat <- swiss |>
specify(Fertility ~ Education) |>
calculate(stat = "correlation")
# Compute bootstrap distribution
infer_boot <-
swiss |>
specify(Fertility ~ Education) |>
generate(reps = 999, type = "bootstrap") |>
calculate(stat = "correlation")
```
I can then calculate studentized, percentile, and bias-corrected bootstrap CIs:
```{r}
CI_normal <- get_confidence_interval(
infer_boot, type = "se",
point_estimate = correlation_hat, level = 0.95
)
CI_percentile <- get_confidence_interval(
infer_boot, type = "percentile",
level = 0.95
)
CI_biascorrected <- get_confidence_interval(
infer_boot, type = "bias-corrected",
point_estimate = correlation_hat, level = 0.95
)
infer_CIs <-
bind_rows(
normal = CI_normal,
percentile = CI_percentile,
`bias-corrected` = CI_biascorrected,
.id = "type"
)
```
For comparison purposes, I'll once again need to re-compute the intervals with `bootstrap_CIs()`, this time with the `infer` bootstrap sample:
```{r}
my_infer_CIs <- bootstrap_CIs(
boot_est = infer_boot$stat,
est = correlation_hat$stat,
CI_type = c("normal","percentile","bias-corrected"),
format = "long"
)
inner_join(my_infer_CIs, infer_CIs)
```
The results do not exactly match across packages. For the normal interval, the difference occurs because the `simhelpers` implementation (like the `boot` implementation) includes a bias-correction term that shifts the interval by the difference between the point estimate and the average bootstrap estimate, which `infer` does not do.
The very small differences in the percentile and bias-corrected intervals are due to the use of different interpolation methods for calculating percentiles.
## `rsample`
Okay, one last time, this time using the [`rsample`](https://rsample.tidymodels.org/) package by @rsamplepkg.
I'll first need to re-work my correlation calculation to provide a `data.frame` with columns called `term`, `estimate`, and `std.error`, and also ensure that the function allows for extra arguments with `...`.
```{r}
rsample_calc_cor <- function(split, ...) {
x <- analysis(split)
n <- nrow(x)
r <- cor(x$Education, x$Fertility)
tibble(
term = "corr",
estimate = r,
std.error = sqrt((1 - r^2)^2 / (n - 1))
)
}
```
Now I can generate a bootstrap distribution using `bootstraps`, setting `apparent = TRUE` to include calculation of the point estimate and analytical standard error. I'll use about 2000 bootstraps here to avoid an automated warning message.
```{r}
library(purrr)
library(tidyr)
library(rsample)
set.seed(20250111)
rsample_boots <-
swiss %>%
bootstraps(1999, apparent = TRUE) %>%
mutate(r = map(splits, rsample_calc_cor))
```
The `resample` package provides functions for calculating percentile, studentized, and BCa intervals. I'll do all three:
```{r}
rsample_CIs <- bind_rows(
int_pctl(rsample_boots, statistics = r),
int_t(rsample_boots, statistics = r),
int_bca(rsample_boots, statistics = r, .fn = rsample_calc_cor)
) %>%
select(type = .method, .lower, .upper) %>%
mutate(
type = recode(type, `student-t` = "student")
)
```
Now I'll redo the interval calculations with `bootstrap_CIs()`:
```{r}
# just the point estimate
rsample_apparent <-
rsample_boots %>%
filter(id == "Apparent") %>%
unnest(r)
# just the bootstraps
rsample_boots <-
rsample_boots %>%
filter(id != "Apparent") %>%
unnest(r)
# jack-knife to get empirical influence values
inf_vals <-
swiss %>%
loo_cv() %>%
mutate(r = map(splits, rsample_calc_cor)) %>%
unnest(r) %>%
mutate(
inf_val = rsample_apparent$estimate - estimate
) %>%
pull(inf_val)
# calculate bootstrap CIs
my_rsample_CIs <-
bootstrap_CIs(
boot_est = rsample_boots$estimate,
boot_se = rsample_boots$std.error,
est = rsample_apparent$estimate,
se = rsample_apparent$std.error,
influence = inf_vals,
CI_type = c("student","percentile","BCa"),
format = "long"
)
# Compare
inner_join(my_rsample_CIs, rsample_CIs)
```
All checks out, with small differences due to the method used to interpolate percentiles and how the acceleration constant is calculated.
Although `rsample` does not provide the full set of bootstrap CI variants, the three it does include are probably the most useful ones.
The option to include the original sample estimate as an additional result in the `bootstraps` object is also quite nice,
and the functions smoothly handle computing bootstraps for each of several terms (such as multiple regression coefficient estimates from a given model).
However, the workflow enforced by `rsample` does seem to have a big downside with respect to memory management.
Taking a bootstrap sample with $B$ replications creates $B$ new datasets (stored in a nested list).
Similarly, running `loo_cv()` creates a near-copy of the dataset for every row of the original dataset.
These could get to be quite large objects:
```{r}
object.size(swiss)
object.size(loo_cv(swiss))
object.size(bootstraps(swiss, times = 999))
```
Especially for large datasets, it would be much more memory-efficient to roll together the re-sampling step and the estimation step or to store only the resampled row indices rather than copies of the full dataset.
# Extrapolating coverage rates a la Boos and Zhang
One big reason that I implemented all these boostrap CI variants in `simhelpers` is to assist with running Monte Carlo simulations of bootstrap procedures.
The main novel feature of my implementation is that `bootstrap_CIs()` can compute not just one interval, but a collection of several intervals using different-sized subsamples of bootstrap replicates.
The number of bootstrap replicates to use in each interval can be specified by providing a vector to the `B_vals` argument, as follows:
```{r}
bootstrap_CIs(
boot_est = cors_boot$r,
boot_se = cors_boot$SE,
est = est["r"],
se = est["SE"],
influence = inf_vals,
CI_type = "BCa",
B_vals = seq(100,1000,100) - 1L,
format = "long"
)
```
In the context of a simulation study, this feature makes it feasible to compute coverage levels of a bootstrap CI for several different values of $B$, then extrapolate to higher numbers of replicates.
## Simulating bootstrap CIs for a Pearson correlation
Here is a small simulation to demonstrate how all this can work.
I'll generate samples of size $n = 25$ from a bivariate-$t$ distribution with correlation parameter $\rho = 0.75$ and with just $\nu = 8$ degrees of freedom. With each sample, I'll calculate the sample correlation and a set of bootstrapped confidence intervals with $B = 49, 99, 199, 299, 399$.
Here's the data-generating function:
```{r}
r_t_bi <- function(n, rho = 0, df = 8) {
Sigma <- rho + diag(1 - rho, nrow = 2)
mvtnorm::rmvt(n = n, sigma = Sigma, df = df)
}
rho <- 0.75
dat <- r_t_bi(25, rho = rho, df = 8)
```
And the estimation function:
```{r}
cor_CI <- function(
dat,
CI_type = "percentile",
B_vals = c(49, 99, 199, 299, 399)
) {
# point estimate
r_est <- cor(dat[,1], dat[,2])
N <- nrow(dat)
SE_r <- sqrt((1 - r_est^2)^2 / (N - 1))
# Fisher z CI
z <- atanh(r_est)
SE_z <- 1 / sqrt(N - 3)
CI_z <- z + c(-1, 1) * qnorm(0.975) * SE_z
# empirical influence if needed
if ("BCa" %in% CI_type) {
jacks <- sapply(1:N, \(x) cor(dat[-x,1], dat[-x,2]))
inf_vals <- r_est - jacks
} else {
inf_vals <- NULL
}
# bootstrap samples
r_boot <- replicate(max(B_vals), {
i <- sample(1:N, replace = TRUE, size = N)
r <- cor(dat[i,1], dat[i,2])
c(r, sqrt((1 - r^2)^2 / (N - 1)))
})
bs_CIs <- simhelpers::bootstrap_CIs(
boot_est = r_boot[1,],
boot_se = r_boot[2,],
est = r_est,
se = SE_r,
influence = inf_vals,
CI_type = CI_type,
B_vals = B_vals,
format = "wide-list"
)
tibble::tibble(
r = r_est,
SE = SE_r,
lo = tanh(CI_z[1]),
hi = tanh(CI_z[2]),
w = mean(r_boot < r_est),
a = sum(inf_vals^3) / (6 * sum(inf_vals^2)^1.5),
bs_CIs = bs_CIs
)
}
res <- cor_CI(dat, CI_type = c("percentile","student"))
res
```
Setting the argument `format = "wide-list"` in the call to `generate_CIs()` makes it convenient to store all the CIs in a nested list-column. Here's the contents of `bs_CIs`:
```{r}
#|
res$bs_CIs[[1]]
```
Now let me pass these functions to `simhelpers::bundle_sim()` so that I can replicate the data-generation and estimation calls as many times as I like.
Calling the resulting function gives me 2000 replications of the whole process, where each replication involves generating $B = 399$ bootstraps and also $n$ leave-one-out jack-knife values:
```{r}
#| cache: true
# bundle the data-generating and estimation functions
# into a simulation driver
sim_cor <- bundle_sim(r_t_bi, cor_CI)
# Run many replications
sim_reps <- sim_cor(
reps = 2000,
n = 25, rho = rho,
B_vals = c(49, 99, 199, 299, 399),
CI_type = c("normal","student","basic","percentile","bias-corrected", "BCa")
)
head(sim_reps)
```
Now I'll summarize across replications to evaluate the coverage rates of each set of confidence intervals. For the Fisher intervals, `simhelpers::calc_coverage()` does the trick, but for the bootstrap intervals I need to use `simhelpers::extrapolate_coverage()` because each replication is a specially structured _set_ of multiple confidence intervals with different values of $B$.
```{r}
perf <-
sim_reps %>%
summarize(
calc_absolute(estimates = r, true_param = rho, criteria = "bias"),
calc_coverage(lower_bound = lo, upper_bound = hi, true_param = rho),
extrapolate_coverage(
CI_subsamples = bs_CIs, true_param = rho,
B_target = 1999,
nested = TRUE, format = "long"
)
)
# Bias and Fisher interval
perf %>%
select(bias, coverage, width)
```
The correlation has a slight negative bias. The Fisher $z$ interval has coverage a bit below nominal and an average width of `{r} round(perf$width, 3)`.
Here is the performance summary of all the percentile intervals:
```{r}
boot_performance <-
perf %>%
select(starts_with("boot")) %>%
unnest(everything())
boot_performance %>%
filter(CI_type == "percentile") %>%
select(CI_type, bootstraps, boot_coverage, boot_width)
```
In addition to the coverage rates and average widths of intervals based on between 49 and 399 bootstraps, the results also include performance summaries for intervals with $B = 1999$ bootstraps, based on the Boos and Zhang extrapolation method.
Here's a graph showing the extrapolated coverage rates for each of the CI variants:
```{r}
#| code-fold: true
#| fig-width: 7
#| fig-height: 4
#| out-width: 100%
boot_performance_top <- filter(boot_performance, bootstraps == 1999)
ggplot(boot_performance) +
aes(x = bootstraps, y = boot_coverage, color = CI_type) +
scale_x_continuous(breaks = c(49,99,199,399,1999), transform = "reciprocal") +
scale_y_continuous(limits = c(0.8,1.0), expand = expansion(0, 0), sec.axis = dup_axis(name = "")) +
geom_hline(yintercept = 0.95, linetype = "dashed") +
geom_hline(data = perf, aes(yintercept = coverage), color = "darkgrey") +
geom_point() +
ggrepel::geom_label_repel(
data = boot_performance_top,
aes(label = CI_type),
nudge_x = -0.004
) +
geom_smooth(method = "lm", formula = y ~ x, se = FALSE) +
theme_minimal() +
theme(legend.position = "none") +
labs(
x = "Bootstraps (B)",
y = "CI coverage rate"
)
```
The studentized interval gets very close to the nominal coverage level with $B = 1999$ bootstraps.
Surprisingly, BCa does not do nearly as well and is worse than the regular percentile interval.
Perhaps this is because, for this simple problem, the extra machinery of the bias and acceleration corrections might not be needed or the corrections cannot be estimated accurately enough with a sample of this size.
Here's the average widths of each variant:
```{r}
#| code-fold: true
#| fig-width: 7
#| fig-height: 4
#| out-width: 100%
boot_performance_bottom <- filter(boot_performance, bootstraps == 49)
ggplot(boot_performance) +
aes(x = bootstraps, y = boot_width, color = CI_type) +
scale_x_continuous(breaks = c(49,99,199,399,1999), transform = "reciprocal") +
geom_hline(data = perf, aes(yintercept = width), color = "darkgrey") +
geom_point() +
ggrepel::geom_label_repel(
data = boot_performance_bottom,
aes(label = CI_type),
nudge_x = 0.004
) +
geom_smooth(method = "lm", formula = y ~ x, se = FALSE) +
theme_minimal() +
theme(legend.position = "none") +
labs(
x = "Bootstraps (B)",
y = "Average CI width"
)
```
The near-nominal coverage rate for the studentized interval comes with an increased width. The percentile and basic CIs have identical widths because they're based on the same percentiles, just used in different ways.
Notably, the percentile interval has shorter average width than the bias-corrected or BCa intervals, even though it also has better coverage.
## Timing
This particular problem is perhaps not the most compelling way illustrate Boos and Zhang's extrapolation method because it would fairly simple to just compute a larger number of bootstraps and not worry about the complications of computing a bunch of extra CIs and extrapolating.
Here's some timing comparisons.
First, the brute-force approach of just computing $B=1999$ bootstraps for each of 500 replications:
```{r}
#| cache: true
library(tictoc)
tic()
perf_1999 <-
sim_cor(
reps = 500,
n = 25, rho = 0.75,
B_vals = 1999,
CI_type = c("normal","student","basic","percentile","bias-corrected", "BCa")
) %>%
unnest(bs_CIs) %>%
pivot_longer(
c(ends_with("_lower"), ends_with("_upper")),
names_pattern = "(.+)_(.+)",
names_to = c("CI_type",".value")
) %>%
group_by(CI_type) %>%
summarize(
calc_coverage(lower_bound = lower, upper_bound = upper, true_param = 0.75)
)
toc()
```
Compare that to doing 500 replications, each with 399 bootstraps but computing 5 confidence intervals each time and then extrapolating out to $B = 1999$:
```{r}
#| cache: true
tic()
perf_extra <-
sim_cor(
reps = 500,
n = 25, rho = 0.75,
B_vals = c(49, 99, 199, 299, 399),
CI_type = c("normal","student","basic","percentile","bias-corrected", "BCa")
) %>%
summarize(
extrapolate_coverage(
CI_subsamples = bs_CIs, true_param = rho,
B_target = 1999,
nested = TRUE, format = "long"
)
)
toc()
```
There is some time savings, but perhaps not worth the extra hassle in this instance.
The extrapolation method is much more useful when the statistic calculated on each bootstrap re-sample takes a relatively long time to compute, so that using only a fraction of the bootstraps (399 versus 1999, in this example) substantially reduces the total compute time.